구매한 책을 읽을때마다, 필요한 키워드를 빠르게 찾고 싶다면 책 뒷편의 부록 페이지에서 인덱스를 살펴볼 것이다. 만약 인덱스가 없더라면, 책에 실린 수많은 텍스트에서 내가 원하는 키워드를 찾아내기 위해 최악의 경우 책 맨 앞에서부터 끝까지를 살펴봐야 한다.
데이터베이스 인덱스
데이터베이스 인덱스는 책 뒷편의 인덱스와 유사한 특징을 가진다. 둘의 공통점은, 내가 원하는 특정 데이터를 빠르게 탐색하기 위해 미리 정렬해놓은 인덱스 정보를 활용하는 것이다. 인덱스를 통해 원하는 데이터가 저장소 내부 어디에 있는지의 정보를 빠르게 서칭하고, 해당 페이지로 이동하여 데이터를 조회할 수 있다.
즉, 데이터베이스 인덱스란 빠른 조회(SELECT) 성능을 위해 미리 저장해놓은 추가적인 저장 공간이다. 마치 책에서 특정 인덱스가 책 본문의 130번 페이지에 원하는 데이터가 존재함을 표현하듯이, 데이터베이스 인덱스는 key 가 20번인 데이터는 테이블 내의 35번째 행에 저장되어 있음을 표현한다.
조회(SELECT) 성능 최적화를 위한 B+ Tree 구조
인덱스는 다양한 방식의 인덱싱 자료구조 저장 형태를 취할 수 있다. 자료구조 종류로는 해싱(Hashing), B- Tree, B+ Tree 등의 형태를 취하지만, 현재 대부분의 데이터베이스에서 취하는 구조는 B+ Tree 이다. 인덱싱 자료구조 및 알고리즘에 대한 내용은 이따가 자세히 학습해보도록 하자.
인덱스는 B+ Tree 자료구조 형태의 저장방식을 취함으로써, 항상 데이터간의 정렬된 상태를 유지한다. 이 구조를 통해 데이터의 저장(INSERT, DELETE, UPDATE) 쿼리 성능을 희생한 대신에, 조회(SELECT) 쿼리 성능을 최적화했다.
인덱스를 왜 사용하는가?
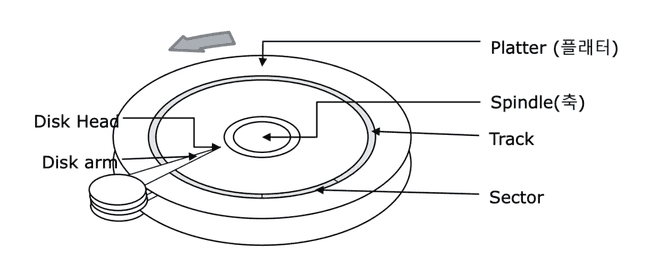
만약 인덱스가 없다면, 우리가 원하는 데이터를 찾기 위해 테이블 풀 스캔(Table Full Scan) 이 발생한다. 테이블 풀 스캔이란, 우리가 원하는 특정 데이터를 찾아내기 위해 데이터베이스의 테이블의 맨 앞부터 끝까지 차례대로 모든 행을 읽어내는 방식이다. 테이블 풀 스캔은 결국 최악의 경우 처음부터 끝 까지 모든 데이터를 탐색해야 하므로, 디스크에서 데이터를 읽어 메모리로 적재하는 I/O 비용이 많이 발생하는 가장 느린 테이블 스캔 방식이다. 데이터베이스는 디스크내에 내장되어 있기 떄문에, 디스크에 직접 접근하여 스캔을 하는 방식대신에 디스크 접근 연산을 최소화하는 방식이 효율적이다.
애당초에 디스크에 접근하여 수행하는 연산은 매우 느리다. 디스크 내부적으로 데이터를 쓰거나 읽기위해 매번 디스크 헤더를 이동시키고, 또 다시 다른 데이터에 대한 연산 처리를 위해 헤더를 이동시켜야 하므로, 비효율적인 연산 구조를 취할 수 밖에없다. 이와 관련한 자세한 내용은 순차 I/O 와 랜덤 I/O 의 차이점에 관련한 내용인데, 향후 다른 포스트에서 자세히 다루도록 하겠다.
반면 인덱스만을 메모리에 B+ Tree 형태로 적재하고, 원하는 데이터를 디스크에서 빠르게 찾아낼 수 있다. 즉, 인덱스를 사용하면 디스크에 접근하여 수행하는 불필요한 I/O 를 최소화하여, 데이터 탐색 성능을 개선할 수 있다. 시간 복잡도 측면에서 테이블 풀 스캔이 최악의 경우 O(N) 의 시간 복잡도를 가진다면, 인덱스는 B+ Tree 구조를 통해 검색 연산시 O(logN) 의 시간복잡도를 가진다. 게다가 인덱스는 자신이 가리키고 있는 실제 데이터에 크기에 비해 매우 작은 크기를 가진다. 따라서 실제 데이터베이스 테이블에 비해 적재하기 용이하다.
인덱스 자료구조
인덱스를 저장하는 자료구조 종류로 해싱(Hashing), B- Tree, B+ Tree 등의 형태를 취하지만, 현재 대부분의 데이터베이스에서 취하는 구조는 B+ Tree 이라고 설몀했다. 각 자료구조의 특징은 어떻게 되길래 현재 대부분의 데이터베이스에서 B+ Tree 구조를 취하게 됐을까?
해시 테이블 (Hash Table)
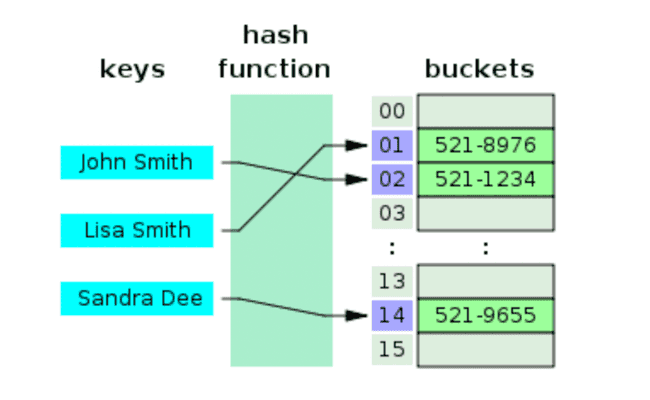
자료구조 전공 수업을 들었다면 한번쯤은 학습해봤을 자료구인 해시 테이블 이다. 해시 테이블은 Key-Value 형태로 데이터르 저장하는 자료구조다. 데이터의 key 값을 알고 있다면, 데이터에 O(1) 라는 빠른 시간 복잡도로 접근할 수 있다.
대소비교 연산으로 인해 느리다
하지만, 해시 테이블은 대소비교 연산에 부적합하기 때문에 DBMS 에서 잘 사용되지 않는 자료구조이다. 해시 테이블의 데이터는 정렬되어 있지 않아서, Key 값이 어떤 기준값보다 크거나 또는 작은 데이터를 찾기 위해선 모든 데이터에 접근해야한다. 즉, N개의 데이터가 있다면 N번의 데이터 접근이 필요하다. 즉, 해시 테이블의 조회 연산은 최악의 경우 O(n) 의 시간이 걸린다. 데이터베이스에서는 대소비교 연산이 자주 발생하기 때문에 해시 테이블은 적합하지 않다.
B- Tree
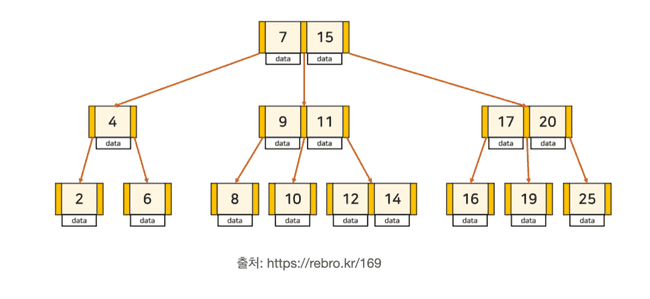
B-Tree 자료구조는 이진트리와 달리 자식 노드를 여러개 가질 수 있는 균형 트리(Balanced Tree) 구조이다. 즉, 이진 탐색 트리의(BST) 에서 자식 노드 개수가 2개 이상으로 확장된 트리 구조다. 이진 탐색 트리의 자식 노드가 최대 2개라면, B-Tree 는 자식 노드가 2개 이상인 트리이다. 이진 탐색 트리에서 노드의 개수를 늘리고 트리의 전체 높이를 줄임으로써 매우 빠른 탐색 성능을 얻을 수 있다.
노드(node)의 종류
트리 내부 노드들의 종류로는, 우선 가장 최상위에는 루트 노드가 존재하며, 맨 하위 계층에는 리프 노드가 존재한다. 또한 이 중간 계층에는 브랜치 노드가 존재한다.
Key-Value 구성
일반적인 이진 트리와 달리, 한 노드에 여러 데이터를 가질 수 있다. B- Tree 구조의 각 노드(node) 는 테이블의 특정 데이터 레코드 행(ex. PK - 기본 키)을 타킷으로 해서, 헤당 행의 값을 key 로, 해당 레코드가 저장된 주소(포인터) 를 value 로 저장하는 일련의 key-value 쌍으로 구성된다.
특히 Key 값의 경우 아무 값이 저장되는 것이 아니라 인덱스가 적용된 컬럼의 값이 저장된다. 예를들어, 테이블의 기본 키(PK) 또는 기타적으로 인덱스를 생성한 컬럼의 값이 Key 값으로 저장된다. 이러한 B-Tree 트리내의 노드들은 마구잡이로 생성되는 것이 아니라, 항상 key 값을 기준으로 오름차순으로 정렬된 상태를 유지한다. 이는 다시말해, 새로운 인덱스가 생성될 때 마다 오름차순 정렬 상태를 유지하기위해 트리내의 노드의 재정렬이 필요함을 뜻한다.
반면 Value 값의 경우 Key 에 해당하는 실제 데이터의 물리적 위치 정보를 저장한다. 즉, Value 값은 Key 에 해당하는 실제 데이터 레코드를 가리키는 포인터를 저장한다.
각 노드는 좌우로 다른 노드를 가리키는 포인터를 가지고있다. 좌측 포인터는 Key 보다 작은 데이터를 가진 노드를 가리키고, 우측 포인터는 Key 보다 큰 데이터를 가진 노드를 가리킨다.
O(logN) 으로 빠르다
B-Tree 는 정렬된 트리 구조이므로 특정 노드를 찾는데 O(logN) 의 시간이 걸린다.
B+ Tree
B+ Tree 는 B- Tree 에서 개선된 구조로, 대부분의 DBMS 에서 채택중인 자료구조이다.
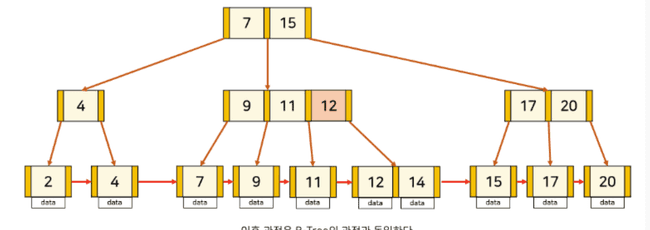
앞선 B- Tree 와 달리, 같은 깊이(depth) 에 존재하는 노드들은 서로 링크드리스트 구조로 연결된 형태를 취한다. 이에따라, 리프 노드끼리도 더블리 링크드리스트로 연결된 구조를 지닌다. 즉, B+ Tree 는 리프 노드끼리 서로를 포인터로 연결하는(가리키는) 링크드 리스트 구조를 취한다. 그리고 이 링크드리스트 구조로 인해 범위 탐색(Range Scan) 의 성능이 매우 빠르다.
리프 노드끼리 링크드 리스트 구조로 연결된다
B+ Tree 는 B-Tree 와 달리 리프 노드끼리 링크드 리스트를 취하기 때문에, 1개가 아닌 여러 데이터를 조회하는 레인지 스캔(Range Scan), 즉 범위 스캔이 유리하다. 데이터배이스 특성상 대소비교 연산이 다소 오래걸리기에, B-Tree 구조 또한 원하는 데이터를 탐색하기 위해 발생하는 여러번의 대소비교 연산 오버헤드를 무시할 수 없었다. 이를 해결하기 위해, B+ Tree 에선 리프 노드를 링크드 리스트(Linked List) 로 연결했다. 즉, 정렬된 상태의 리프 노드 중에서 원하는 몇몇 데이터(노드)들을 맨 앞에서부터 차례대로 빠르게 순차 탐색(Sequential Search) 으로 찾아낼 수 있게된다.
만약 B- Tree 를 레인지 스캔하면 어떤 과정이 일어날까? 원하는 데이터 N개를 찾아내기 위해, 각 데이터에 대해 매번 루트 노드부터 시작하여 리프 노드까지 대소 비교를 하는 연산이 N번 발생할 것이다. 반면, B+ Tree 의 경우 루트 노드에서 특정 리프 노드에 한 번 도달한 뒤, 해당 리프 노드에서부터 시작해서 링크드리스트를 따라 넘어가면서 여러 리프노드를 따라 순차 탐색하면 된다.
인덱스를 모든 컬럼에 적용해도 될까?
궁금증이 하나 생긴다. 이런 장점을 지닌 인덱스를 데이터베이스 테이블내에 적용하면 조회 쿼리 성능이 매우 좋아지는게 아닐까? 인덱스를 항상 모든 테이블에 적용하면 안될까? 하지만, 이런 인덱스도 이곳저곳에 모두 적용하고 남발하면 되려 역효과를 볼 수 있다.
인덱스를 생성하면, 아무곳에나 생성되는 것이 아니라 데이터베이스내에서 인덱스가 생성되는 특정 공간이 고정되어있다. 이 저장 공간은 데이터베이스 전체 공간에서 최대 약 10% 만을 허용한다. 즉, 인덱스를 생성할 수 있는 저장공간의 크기는 매우 작기 때문에, 잘못 사용하면 불필요한 저장 공간을 낭비할 수 있다.
카디널리티(Cardinality) 를 고려하여 정말 필요한 컬럼만 인덱스를 적용할 것
따라서 인덱스는 정말 필요한 컬럼에 대해서만 적용하는 것이 바람직하다. 그렇다면, 인덱스를 효율적으로 적용하기 위한 기준은 무엇이 있을까?
바로 카디널리티(Cardinality) 이다. 카디널리티란 데이터 집합에서 유일한 데이터 개수를 뜻한다. 즉, 데이터 특성상 유일성이 높은 컬럼일수록 인덱싱해주는 것이 좋다. 예를들어, 성별 컬럼보다 주민등록번호 컬럼의 카디널리티가 매우 높을 것이다. 성별은 모든 사람이 남/여 2가지 값 중 하나를 가지기 때문에, 유일성 수치가 매우 낮다. 반면 주민등록번호는 단 1명의 사람에게 보장되는 유일성을 가지기 떄문에 카디널리티가 높다.
삽입, 수정, 삭제가 자주 발생하는 컬럼에는 적용하지 말 것
INSERT, UPDATE, DELETE 등의 데이터 구성에 변동을 줄 쿼리가 자주 사용되는 컬럼에 대해선 인덱스를 적용하지 않는 것이 좋다. 즉, 조회 연산만 자주 발생하는 컬럼에 대해서 인덱싱하는 것이 좋다. 앞서 설명했듯이, B+ Tree 구조는 새로운 인덱스가 생성 및 수정, 삭제될 때 마다 오름차순 정렬 상태를 유지하기위해 트리내의 노드의 재정렬이 필요하다. 재정렬 시간은 꽤 오래걸리며, 인덱스는 조회 성능을 최적화하는데 초점이 맞춰져있음을 기억하자.